Algrithm: Sort
O(n2) algorithms
1.Bubble Sort
The algorithm works by comparing each item in the list with the item next to it, and swapping them if required. In other words, the largest element has bubbled to the top of the array. The algorithm repeats this process until it makes a pass all the way through the list without swapping any items.
void bubbleSort(int ar[])
{
for (int i = (ar.length - 1); i >= 0; i--)
{
for (int j = 1; j ≤ i; j++)
{
if (ar[j-1] > ar[j])
{
int temp = ar[j-1];
ar[j-1] = ar[j];
ar[j] = temp;
} } } }
Example. Here is one step of the algorithm. The largest element - 7 - is bubbled to the top:
7, 5, 2, 4, 3, 9 5, 7, 2, 4, 3, 9 5, 2, 7, 4, 3, 9 5, 2, 4, 7, 3, 9 5, 2, 4, 3, 7, 9 5, 2, 4, 3, 7, 9
The worst-case runtime complexity is O(n2).
2.Selection Sort
Step 1 − Set MIN to location 0 Step 2 − Search the minimum element in the list Step 3 − Swap with value at location MIN Step 4 − Increment MIN to point to next element Step 5 − Repeat until list is sorted
void selectionSort(int[] ar){
for (int i = 0; i ‹ ar.length-1; i++)
{
int min = i;
for (int j = i+1; j ‹ ar.length; j++)
if (ar[j] ‹ ar[min]) min = j;
int temp = ar[i];
ar[i] = ar[min];
ar[min] = temp;
} }
Example: Red: Minimum value found in left array Yellow: Min location ( the first position in unsorted-array) Swap red and yellow 29, 64, 73, 34, 20 20, 64, 73, 34, 29 20, 29, 73, 34, 64 20, 29, 34, 73, 64 20, 29, 34, 64, 73
The worst-case runtime complexity is O(n2).
3.Insertion Sort
Step 1 − Assume first element is already sorted; Step 2 − Pick from second element to end; Step 3 − Compare with all elements in the sorted sub-array, the sub-array befroe Target. compare from [j-1] to 0; Step 4 − Shift all the elements (move to [j], inorder to leave old [j-1] to Target) in the sorted sub-array that is greater than the Target. Step 5 − Insert the Target to j ( Target > ar[j-1] and set ar[j] = Target or compare to 0, set ar[0] = target); Step 6 − Repeat until array is sorted
void insertionSort(int[] ar)
{
for (int i=1; i ‹ ar.length; i++)
{
int target = ar[i]; int j = i;
while (j > 0 && ar[j-1] > target)
{
ar[j] = ar[j-1];
j--;
}
ar[j] = target;
} }
Example: Yellow: sorted sub-array Red: Target 29, 20, 73, 34, 64 20, 29, 73, 34, 64 20, 29, 73, 34, 64 20, 29, 34, 73, 64 20, 29, 34, 64, 73
The worst-case runtimecomplexity is O(n2). The best-case runtime complexity: O(n)
O(n log n) algorithms
1.Merge Sort
Merge-sort is based on the divide-and-conquer paradigm. It involves the following three steps:
- Divide the array into two (or more) subarrays
- Sort each subarray (Conquer)
- Merge them into one (in a smart way!)
Example. Consider the following array of numbers 27 10 12 25 34 16 15 31 divide it into two parts 27 10 12 25 34 16 15 31 divide each part into two parts 27 10 12 25 34 16 15 31 divide each part into two parts 27 10 12 25 34 16 15 31 How do we merge two sorted subarrays? We define three references at the front of each array. We keep picking the smallest element and move it to a temporary array, incrementing the corresponding indices. merge (cleverly-!) parts 10 27 12 25 16 34 15 31 merge parts 10 12 25 27 15 16 31 34 10 10 12 25 27 15 16 31 34 10 12 10 12 25 27 15 16 31 34 10 12 15 merge parts into one 10 12 15 16 25 27 31 34
import java.util.*;
public class MergerSort
{
public static void main(String[] args)
{
Integer[] a = {2, 6, 3, 5, 1};
mergeSort(a);
System.out.println(Arrays.toString(a));
}
public static void mergeSort(Comparable [ ] a)
{
Comparable[] tmp = new Comparable[a.length];
mergeSort(a, tmp, 0, a.length - 1);
}
private static void mergeSort(Comparable [ ] a, Comparable [ ] tmp, int left, int right)
{
//don't have base case
//don't need to return
if( left < right )
{
int center = (left + right) / 2;
mergeSort(a, tmp, left, center);
mergeSort(a, tmp, center + 1, right);
merge(a, tmp, left, center + 1, right);
}
}
private static void merge(Comparable[ ] a, Comparable[ ] tmp, int left, int right, int rightEnd )
{
int leftEnd = right - 1;
int k = left;
int num = rightEnd - left + 1;
while(left <= leftEnd && right <= rightEnd)
if(a[left].compareTo(a[right]) <= 0)
//k represent these two sub-array position in the old array
tmp[k++] = a[left++];
else
tmp[k++] = a[right++];
while(left <= leftEnd) // Copy rest of first half
tmp[k++] = a[left++];
while(right <= rightEnd) // Copy rest of right half
tmp[k++] = a[right++];
// Copy tmp back
//tmp represent new array to store new order sub-array
for(int i = 0; i < num; i++, rightEnd--)
a[rightEnd] = tmp[rightEnd];
}
}
2.Quick Sort
Quick sort is based on the divide-and-conquer approach based on the idea of choosing one element as a pivot element and partitioning the array around it such that: Left side of pivot contains all the elements that are less than the pivot element Right side contains all elements greater than the pivot
Implementation : Select the first element of array as the pivot element First, we will see how the partition of the array takes place around the pivot.
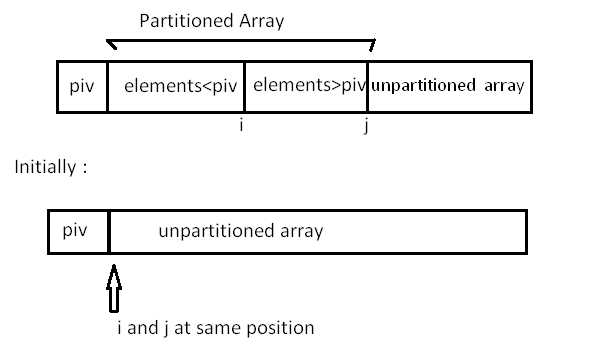
In the implementation below, the following components have been used: Here, A[] = array whose elements are to be sorted start: Leftmost position of the array end: Rightmost position of the array i: Boundary between the elements that are less than pivot and those greater than pivot j: Boundary between the partitioned and unpartitioned part of array piv: Pivot element
int partition ( int A[],int start ,int end) {
int i = start + 1;
int piv = A[start] ; //make the first element as pivot element.
for(int j =start + 1; j <= end ; j++ ) {
/*rearrange the array by putting elements which are less than pivot
on one side and which are greater that on other. */
if ( A[ j ] < piv) {
swap (A[ i ],A [ j ]);
i += 1;
}
}
swap ( A[ start ] ,A[ i-1 ] ) ; //put the pivot element in its proper place.
return i-1; //return the position of the pivot
}
Now, let us see the recursive function Quick_sort :
void quick_sort ( int A[ ] ,int start , int end ) {
if( start < end ) {
//stores the position of pivot element
int piv_pos = partition (A,start , end ) ;
quick_sort (A,start , piv_pos -1); //sorts the left side of pivot.
quick_sort ( A,piv_pos +1 , end) ; //sorts the right side of pivot.
}
}
//Let’s see the randomized version of the partition function :
//Some also set pivot as last one or check the mid value of first, last and mid
int rand_partition ( int A[ ] , int start , int end ) {
//chooses position of pivot randomly by using rand() function .
int random = start + rand( )%(end-start +1 ) ;
swap ( A[random] , A[start]) ; //swap pivot with 1st element.
return partition(A,start ,end) ; //call the above partition function
}
O(n) algorithms
1.Counting Sort
Let’s assume that, array of size needs to be sorted.
- Initialize the auxillary array Aux[] as 0.
Note: The size of this array should be . - Traverse array A and store the count of occurrence of each element in the appropriate index of the Aux array, which means, execute Aux[ A[ i ] ]++ for each i, where i ranges from [0, N-1].
- Initialize the empty array sortedA[]
- Traverse array Aux and copy i into sortedA for Aux[ i ] number of times where 0 <= i <= max[ A[] ]>.
Note: The array A can be sorted by using this algorithm only if the maximum value in array A is less than the maximum size of the array Aux. Usually, it is possible to allocate memory up to the order of a million ( 10 6). If the maximum value of exceeds the maximum memory- allocation size, it is recommended that you do not use this algorithm. Use either the quick sort or merge sort algorithm.
Implementation: Assume that the maximum element that can be in the array is K. Now take an Aux[] array of size K+1. A[] = Array to be sorted. sortedA[] = Sorted version of A[].
void counting_sort(int A[], int Aux[], int sortedA[], int N) {
// First, find the maximum value in A[]
int K = 0;
for(int i=0; i<N; i++) {
K = max(K, A[i]);
}
// Initialize the elements of Aux[] with 0
for(int i=0 ; i<=K; i++) {
Aux[i] = 0;
}
// Store the frequencies of each distinct element of A[],
// by mapping its value as the index of Aux[] array
for(int i=0; i<N; i++) {
Aux[A[i]]++;
}
int j = 0;
for(int i=0; i<=K; i++) {
int tmp = Aux[i];
// Aux stores which element occurs how many times,
// Add i in sortedA[] according to the number of times i occured in A[]
while(tmp--) {
//cout << Aux[i] << endl;
sortedA[j] = i;
j++;
}
}
}
Example:
Say A={5, 2, 9, 5, 2, 3, 5}.
Aux will be of the size 9 + 1 i.e 10.
Aux = {0, 0, 2, 1, 0, 3, 0, 0, 0, 2}.
Notice that Aux[2] = 2 which represents the number of occurrences of 2 in A[]. Similarly Aux[5] = 3 which represents the number occurrences of 5 in A[].
After applying the counting sort algorithm, sortedA[] will be {2, 2, 3, 5, 5, 5, 9}
Time Complexity:
The array A is traversed in O(N) time and the resulting sorted array is also computed in O(N) time. Aux is traversed in O(K) time. Therefore, the overall time complexity of counting sort algorithm is O(N+K).
2.Radix Sort
Prerequisite: Counting Sort
QuickSort, MergeSort, HeapSort are comparison based sorting algorithms.
CountSort is not comparison based algorithm. It has the complexity of O(N+K), where K is the maximum element of the input array.
So, if K is O(N),CountSort becomes linear sorting, which is better than comparison based sorting algorithms that have time O(nlogn)complexity. The idea is to extend the CountSort algorithm to get a better time complexity when k goes (N2). Here comes the idea of Radix Sort.
Algorithm:
For each digit i where i varies from the least significant digit to the most significant digit of a number
Sort input array using countsort algorithm according to ith digit.
We used count sort because it is a stable sort.
Example: Assume the input array is: 10,21,17,34,44,11,654,123 Based on the algorithm, we will sort the input array according to the one's digit (least significant digit). 0: 10 1: 21 11 2: 3: 123 4: 34 44 654 5: 6: 7: 17 8: 9: So, the array becomes 10,21,11,123,24,44,654,17 Now, we'll sort according to the ten's digit: 0: 1: 10 11 17 2: 21 123 3: 34 4: 44 5: 654 6: 7: 8: 9: Now, the array becomes : 10,11,17,21,123,34,44,654 Finally , we sort according to the hundred's digit (most significant digit): 0: 010 011 017 021 034 044 1: 123 2: 3: 4: 5: 6: 654 7: 8: 9: The array becomes : 10,11,17,21,34,44,123,654 which is sorted. This is how our algorithm works.
Implementation:
void countsort(int arr[],int n,int place)
{
int i,freq[range]={0}; //range for integers is 10 as digits range from 0-9
int output[n];
for(i=0;i<n;i++)
freq[(arr[i]/place)%range]++;
for(i=1;i<range;i++)
freq[i]+=freq[i-1];
for(i=n-1;i>=0;i--)
{
output[freq[(arr[i]/place)%range]-1]=arr[i];
freq[(arr[i]/place)%range]--;
}
for(i=0;i<n;i++)
arr[i]=output[i];
}
void radixsort(ll arr[],int n,int maxx) //maxx is the maximum element in the array
{
int mul=1;
while(maxx)
{
countsort(arr,n,mul);
mul*=10;
maxx/=10;
}
}
Complexity Analysis:
The complexity is O((n+b)*logb(max x)) where b is the base(binary or decimal) for representing numbers and max x is the maximum element of the input array. This is clearly visible as we make (n+b) iterations logb(max x) times (number of digits in the maximum element) . If max x <= nc,then the complexity can be written as O(n*logb(n )).
Advantages :
1. Fast when the keys are short i.e. when the range of the array elements is less.
2. Used in suffix array constuction algorithms like Manber's algorithm and DC3 algorithm.
Disadvantages :
1. Since Radix Sort depends on digits or letters, Radix Sort is much less flexible than other sorts. Hence , for every different type of data it needs to be rewritten.
2. The constant for Radix sort is greater compared to other sorting algorithms.
3. It takes more space compared to Quicksort which is inplace sorting.
The Radix Sort algorithm is an important sorting algorithm that is integral to suffix -array construction algorithms. It is also useful on parallel machines.
3.Bucket Sort
Bucket sort is a comparison sort algorithm that operates on elements by dividing them into different buckets and then sorting these buckets individually. Each bucket is sorted individually using a separate sorting algorithm or by applying the bucket sort algorithm recursively. Bucket sort is mainly useful when the input is uniformly distributed over a range.
void bucketSort(float[] a,int n)
{
for(each floating integer 'x' in n)
{
insert x into bucket[n*x];
}
for(each bucket)
{
sort(bucket);
}
}
If one assumes that insertion in a bucket takes O(1) time, then steps 1 and 2 of the above algorithm clearly take O(N) time. But we dont know how much buckets we have, and sort() method time complexity.
JAVA Arrays
1.Arrays.sort()
Dual-Pivot Quick Sort:
sort(int[] a) sort(int[] a, int fromIndex, int toIndex) Same as: long[], short[], char[], byte[], float[], double[]
Tim Sort:
sort(Object[] a) sort(Object[] a, int fromIndex, int toIndex) sort(T[] a, Comparator<? super T> c) sort(T[] a, int fromIndex, int toIndex, Comparator<? super T> c)
public static void main(String[] args)
{
// Our arr contains 8 elements
int[] arr = {13, 7, 6, 45, 21, 9, 101, 102};
Arrays.sort(arr);
System.out.printf("Modified arr[] : %s",
Arrays.toString(arr));
}
//Output: Modified arr[] : [6, 7, 9, 13, 21, 45, 101, 102]
public static void main(String[] args)
{
// Our arr contains 8 elements
int[] arr = {13, 7, 6, 45, 21, 9, 2, 100};
// Sort subarray from index 1 to 4, i.e.,
// only sort subarray {7, 6, 45, 21} and
// keep other elements as it is.
Arrays.sort(arr, 1, 5);
System.out.printf("Modified arr[] : %s",
Arrays.toString(arr));
}
//Modified arr[] : [13, 6, 7, 21, 45, 9, 2, 100]
public static void main(String[] args)
{
String arr[] = {"practice.geeksforgeeks.org",
"quiz.geeksforgeeks.org",
"code.geeksforgeeks.org"
};
// Sorts arr[] in ascending order
Arrays.sort(arr);
System.out.printf("Modified arr[] : \n%s\n\n",
Arrays.toString(arr));
// Sorts arr[] in descending order
Arrays.sort(arr, Collections.reverseOrder());
System.out.printf("Modified arr[] : \n%s\n\n",
Arrays.toString(arr));
}
// Modified arr[] :
// [code.geeksforgeeks.org, practice.geeksforgeeks.org, quiz.geeksforgeeks.org]
// Modified arr[] :
// [quiz.geeksforgeeks.org, practice.geeksforgeeks.org, code.geeksforgeeks.org]
// Java program to demonstrate working of Comparator
// interface
import java.util.*;
import java.lang.*;
import java.io.*;
// A class to represent a student.
class Student
{
int rollno;
String name, address;
// Constructor
public Student(int rollno, String name,
String address)
{
this.rollno = rollno;
this.name = name;
this.address = address;
}
// Used to print student details in main()
public String toString()
{
return this.rollno + " " + this.name +
" " + this.address;
}
}
class Sortbyroll implements Comparator<Student>
{
// Used for sorting in ascending order of
// roll number
public int compare(Student a, Student b)
{
return a.rollno - b.rollno;
}
}
// Driver class
class Main
{
public static void main (String[] args)
{
Student [] arr = {new Student(111, "bbbb", "london"),
new Student(131, "aaaa", "nyc"),
new Student(121, "cccc", "jaipur")};
System.out.println("Unsorted");
for (int i=0; i<arr.length; i++)
System.out.println(arr[i]);
Arrays.sort(arr, new Sortbyroll());
System.out.println("\nSorted by rollno");
for (int i=0; i<arr.length; i++)
System.out.println(arr[i]);
}
}
// Unsorted
// 111 bbbb london
// 131 aaaa nyc
// 121 cccc jaipur
// Sorted by rollno
// 111 bbbb london
// 121 cccc jaipur
// 131 aaaa nyc
2.Arrays.parallelSort()
sort(int[] a) sort(int[] a, int fromIndex, int toIndex) Same as: long[], short[], char[], byte[], float[], double[] parallelSort(T[] a) parallelSort(T[] a, Comparator<? super T> cmp) parallelSort(T[] a, int fromIndex, int toIndex) parallelSort(T[] a, int fromIndex, int toIndex, Comparator<? super T> cmp)
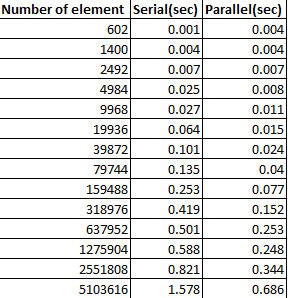
Parallel sort uses threading (each thread gets a chunk of the list and sorts it in parallel. Later these sorted chunks are merged into a result). It's faster when there are a lot of elements in the collection. The overhead for parallelization becomes tolerably small on larger arrays, but it is large for smaller ones.
JAVA ArrayList/LinkedList
Consider an ArrayList that stores country names as String objects. To sort the ArrayList, you need to simply call the Collections.sort() method passing the ArrayList object populated with country names. This method will sort the elements (country names) of the ArrayList using natural ordering (alphabetically in ascending order)
Collections.sort:
adapted from Tim Peters’s list sort for Python ( TimSort)
java.util.Collections.reverseOrder()
ArrayList<String> countryList = new ArrayList<>();
countryList.add("France");
countryList.add("USA");
countryList.add("India");
countryList.add("Spain");
countryList.add("England");
System.out.println("Unsorted ArrayList: " + countryList);
Collections.sort(countryList);
System.out.println("Sorted ArrayList in Ascending Order : " + countryList);
Collections.sort(countryList, Collections.reverseOrder());
System.out.println("Sorted ArrayList in Descending Order: " + countryList);
// Unsorted ArrayList: [France, USA, India, Spain, England]
// Sorted ArrayList in Ascending Order : [England, France, India, Spain, USA]
// Sorted ArrayList in Descending Order: [USA, Spain, India, France, England]
public static Comparator reverseOrder(Comparator c)
class Student
{
int rollno;
String name, address;
// Constructor
public Student(int rollno, String name,
String address)
{
this.rollno = rollno;
this.name = name;
this.address = address;
}
// Used to print student details in main()
public String toString()
{
return this.rollno + " " + this.name +
" " + this.address;
}
}
class Sortbyroll implements Comparator<Student>
{
// Used for sorting in ascending order of
// roll number
public int compare(Student a, Student b)
{
return a.rollno - b.rollno;
}
}
// Driver class
class Main
{
public static void main (String[] args)
{
ArrayList<Student> ar = new ArrayList<Student>();
ar.add(new Student(111, "bbbb", "london"));
ar.add(new Student(131, "aaaa", "nyc"));
ar.add(new Student(121, "cccc", "jaipur"));
System.out.println("Unsorted");
for (int i=0; i<ar.size(); i++)
System.out.println(ar.get(i));
// Sorting a list of students in descending order of
// roll numbers using a Comparator that is reverse of
// Sortbyroll()
Comparator c = Collections.reverseOrder(new Sortbyroll());
Collections.sort(ar, c);
System.out.println("\nSorted by rollno");
for (int i=0; i<ar.size(); i++)
System.out.println(ar.get(i));
}
}
// Unsorted
// 111 bbbb london
// 131 aaaa nyc
// 121 cccc jaipur
// Sorted by rollno
// 131 aaaa nyc
// 121 cccc jaipur
// 111 bbbb london
Reference
https://www.cs.cmu.edu/~adamchik/15-121/lectures/Sorting%20Algorithms/sorting.html
https://medium.com/@george.seif94/a-tour-of-the-top-5-sorting-algorithms-with-python-code-43ea9aa02889
https://www.tutorialspoint.com/
https://www.hackerearth.com
https://www.geeksforgeeks.org
https://stackoverflow.com
https://dzone.com/articles/sorting-java-arraylist
